Elliptic Curve Cryptography

Elliptic Curve Cryptography (ECC) is an asymmetric cryptographic protocol that, like RSA and Diffie-Hellman (DH), relies on a trapdoor function. To recap: trapdoor functions allow a client to keep data secret by performing a mathematical operation which is computationally easy to do, but currently understood to be very expensive to undo.

For RSA, the trapdoor function relies on the hardness of factoring large numbers. For Diffie-Hellman, the trapdoor relies on the hardness of the discrete log problem. For both RSA and DH, the operations that run through the veins of the protocol are familiar to us. Multiplying numbers and taking powers of numbers are things we are taught to do in school. ECC stands out, because the group operation in ECC won't pop up in your life unless you are looking for it.

This discussion here will not be total, and those who are really looking to understand ECC, I recommend these notes Elliptic Curve notes by Ben Lynn, and the textbook "An Introduction to Mathematical Cryptography", Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman.


Let's start thinking about ECC by looking at what we mean by an elliptic curve. We will be studying Weierstrass equations, which are of the form

Y2 = X3 + a X + b

Elliptic curves have an amazing feature: we can define an operator that we will call "point addition". This operator takes two points on some curve and produces a third point on the curve. Taking the set of points on an elliptic curve, point addition defines an Abelian group operation.

There's a lot of text here. Let's motivate this! We can understand scalar multiplication of a point as the repeated point addition of the same point. Q = 2 P = P + P. It turns out that scalar multiplication is a trapdoor function! ECC relies on the hardness of finding the n such that Q = nP given Q and P.


So how do we understand point addition?

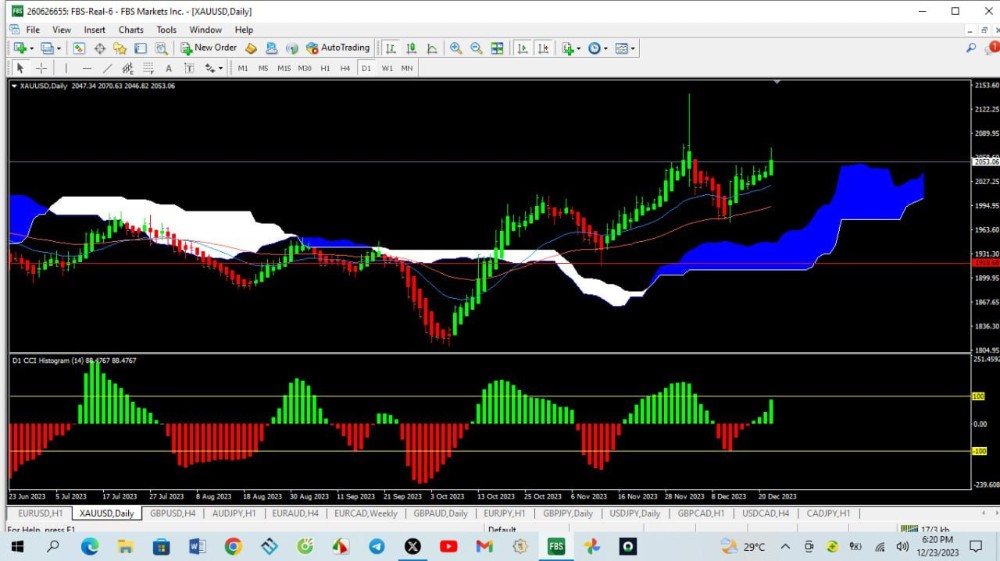
Geometrically, we can understand point addition P + Q like so. Take an elliptic curve and mark the two points P, Q along the curve with their x,y coordinates. Draw a straight line that passes through both points. Now continue the line until it intersects your curve a third time. Mark this new intersection R. Finally, take R and reflect it along the y direction to produce R' = R(x,-y). The result of the point addition is P + Q = R'

What if we want to add two of the same point together: P + P? We can't draw a unique line through one point, but we can pick a unique line by calculating the tangent line to the curve at the point. Calculate the tangent line at the point P. Continue the line until it intersects with the curve at point R. Reflect this point as before: P + P = R' = R(x,-y).

What happens if there is no third intersection? Sometimes you will pick two points P, Q and the line will not touch the curve again. In this case we say that the line intersects with the point (O) which is a single point located at the end of every vertical line at infinity. As such, point addition for an elliptic curve is defined in 2D space, with an additional point located at infinity.

Included below is a diagram as a visual aid to these different cases

The point O acts as the identity operator of the group: P + O = P and P + (-P) = O.

This brings us to the point of defining an elliptic curve.

Definition: An elliptic curve E is the set of solutions to a Weierstrass equation

E: Y2 = X3 + a X + b

together with a point at infinity O. The constants a,b must satisfy the relationship

4a3 + 27 b2 ≠ 0

to ensure there are no singularities on the curve.

Formally, let E be an elliptic curve, point addition has the following properties

(a) P + O = O + P = P
(b) P + (−P) = O
(c) (P + Q) + R = P + (Q + R)
(d) P + Q = Q + P

In ECC, we study elliptic curves over a finite field Fp. This means we look at the curve modulo the characteristic p and an elliptic curve will no longer be a curve, but a collection of points whose x,y coordinates are integers in Fp.

The following starter challenges will take you through the calculations for ECC and get you used to the basic operations that ECC is built upon, have fun!

Property (d) shows that point addition is commutative. The flag is the name we give groups with a commutative operation.

In the background section, we covered the basics of how we can view point addition over an elliptic curve as being an abelian group operation. In this geometric picture we allowed the coordinates on the curve to be any real number.

To apply elliptic curves in a cryptographic setting, we study elliptic curves which have coordinates in a finite field Fp.

We will still be considering elliptic curves of the form E: Y2 = X3 + a X + b , which satisfy the following conditions: a,b ∈ Fp and 4a3 + 27 b2 ≠ 0. However, we no longer think of the elliptic curve as a geometric object, but rather a set of points defined by

E(Fp) = {(x,y) : x,y ∈ Fp satisfying: y2 = x3 + a x + b} ∪ O

 Note: Everything we covered in the background still holds. The identity of the group is the point at infinity: O, and the addition law is unchanged. Given two points in E(Fp), the addition law will generate another point in E(Fp).


For all the challenges in the starter set, we will be working with the elliptic curve

E: Y2 = X3 + 497 X + 1768, p: 9739

Using the above curve, and the point P(8045,6936), find the point Q(x,y) such that P + Q = O.

 Remember, we're working in a finite field now, so you'll need to work correctly with negative numbers.



Resources:
 - The Animated Elliptic Curve: Visualizing Elliptic Curve Cryptography