Fibonacci Retracement Levels part 1

What Are Fibonacci Retracement Levels?

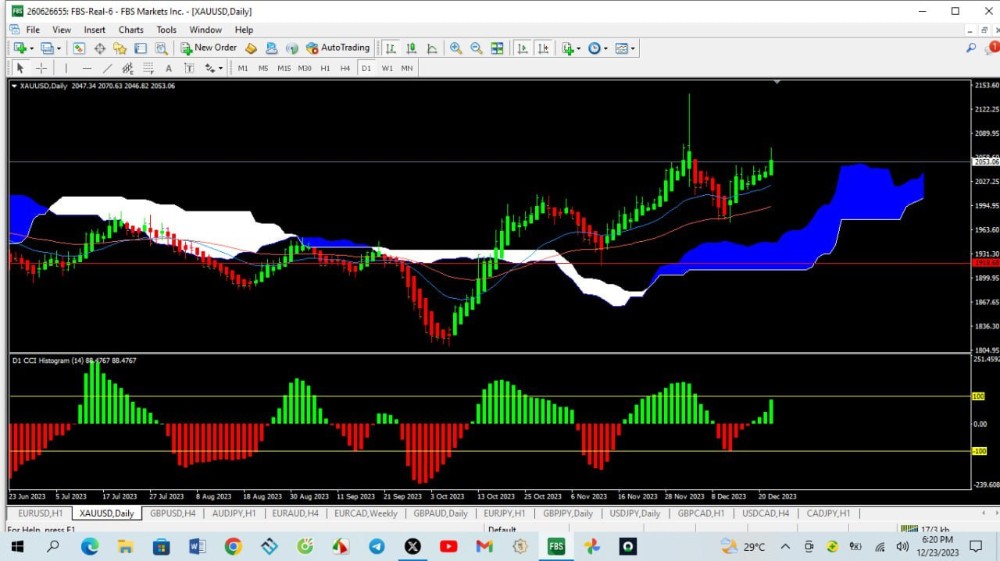
Fibonacci retracement levels—stemming from the Fibonacci sequence—are horizontal lines that indicate where support and resistance are likely to occur.
Each level is associated with a percentage. The percentage is how much of a prior move the price has retraced. The Fibonacci retracement levels are 23.6%, 38.2%, 61.8%, and 78.6%. While not officially a Fibonacci ratio, 50% is also used.
The indicator is useful because it can be drawn between any two significant price points, such as a high and a low. The indicator will then create the levels between those two points.
Suppose the price of a stock rises $10 and then drops $2.36. In that case, it has retraced 23.6%, which is a Fibonacci number. Fibonacci numbers are found throughout nature. Therefore, many traders believe that these numbers also have relevance in financial markets.
Fibonacci retracement levels were named after Italian mathematician Leonardo Pisano Bigollo, who was famously known as Leonardo Fibonacci.  However, Fibonacci did not create the Fibonacci sequence. Instead, Fibonacci introduced these numbers to western Europe after learning about them from Indian merchants.1
 Fibonacci retracement levels were formulated in ancient India between 450 and 200 BCE.

KEY TAKEAWAYS

• Fibonacci retracement levels connect any two points that the trader views as relevant, typically a high point and a low point.
• The percentage levels provided are areas where the price could stall or reverse.
• The most commonly used ratios include 23.6%, 38.2%, 50%, 61.8%, and 78.6%.
• These levels should not be relied on exclusively, so it is dangerous to assume that the price will reverse after hitting a specific Fibonacci level.
• Fibonacci numbers and sequencing were first used by Indian mathematicians centuries before Leonardo Fibonacci.

Numbers First Formulated in Ancient India

Despite its name, the Fibonacci sequence was not developed by its namesake. Instead, centuries before Leonardo Fibonacci shared it with western Europe, it was developed and used by Indian mathematicians.

Most notably, Indian mathematician Acarya Virahanka is known to have developed Fibonacci numbers and the method of their sequencing around 600 A.D.2
 Following Virahanka’s discovery, other subsequent generations of Indian mathematicians—Gopala, Hemacandra, and Narayana Pandita—referenced the numbers and method. Pandita expanded its use by drawing a correlation between the Fibonacci numbers and multinomial co-efficients.
It is estimated that Fibonacci numbers existed in Indian society as early as 200 B.C.3

The Formula for Fibonacci Retracement Levels

Fibonacci retracement levels do not have formulas. When these indicators are applied to a chart, the user chooses two points. Once those two points are chosen, the lines are drawn at percentages of that move.
Suppose the price rises from $10 to $15, and these two price levels are the points used to draw the retracement indicator. Then, the 23.6% level will be at $13.82 ($15 - ($5 × 0.236) = $13.82). The 50% level will be at $12.50 ($15 - ($5 × 0.5) = $12.50).

How to Calculate Fibonacci Retracement Levels

As discussed above, there is nothing to calculate when it comes to Fibonacci retracement levels. They are simply percentages of whatever price range is chosen.
However, the origin of the Fibonacci numbers is fascinating. They are based on something called the Golden Ratio. Start a sequence of numbers with zero and one. Then, keep adding the prior two numbers to get a number string like this:

• 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...with the string continuing indefinitely.

The Fibonacci retracement levels are all derived from this number string. After the sequence gets going, dividing one number by the next number yields 0.618, or 61.8%. Divide a number by the second number to its right, and the result is 0.382 or 38.2%. All the ratios, except for 50% (since it is not an official Fibonacci number), are based on some mathematical calculation involving this number string.
The Golden Ratio, known as the divine proportion, can be found in various spaces, from geometry to human DNA.
Interestingly, the Golden Ratio of 0.618 or 1.618 is found in sunflowers, galaxy formations, shells, historical artifacts, and architecture.